|
| |||||||||||
|
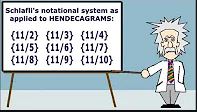
Hendecagram (Eleven-Pointed Star) A Swiss mathematician by the name of Ludwig Schlafli developed a notational system that defines all sorts of interesting shapes. For this discussion we are only interested in eleven-pointed stars. However, Schlafli's notational system can be used to define all sorts of complicated geometric patterns. As for hendecagrams, the notation always includes an eleven in the first spot, but the second number can be any number from two to ten, like so:
{11/2} {11/3} {11/4} {11/5} {11/6} {11/7} {11/8} {11/9}
By the way, {11/1} denotes a hendecagon, for your information. So, it's easy
to see that the first number in this notation corresponds to the number of
vertices in a hendecagram or hendecagon. What is less obvious, is that the
second number defines the number of vertices skipped when connecting
vertices. So, applying this idea, it's easy to see why {11/1} defines a
hendecagon. Watch the video carefully and this system will make sense as it
applies to hendecagrams and other two dimensional objects.
|
Watch video on this page at YouTube! | ||||||||||
|
| |||||||||||
|
| |||||||||||

|
Lyrics:
Eleven-pointed star
Hendecagrams are eleven-pointed |
Blackturtle.us Main Page